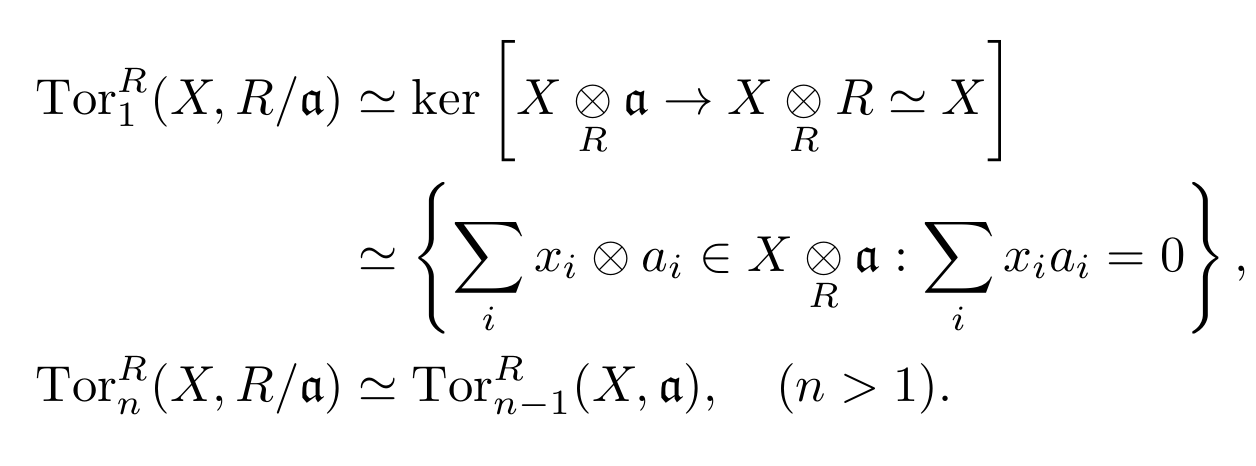Ext functor and Tor functor

这一节Ext函子和Tor函子, 大部分内容是上一章的直接推论, 唯一一个不平凡的定理择时对双函子Hom导出会得到相同的结果. 本节后半部分是关于这俩导出函子的计算的, 这俩函子的计算十分富有技巧性, 全写上来会很长. 最后部分的表格参考了Xiong Rui的小册子.

We consider category with enough projectives, e.g. $\mathrm{Mod}$ .

Functor $\mathrm{Ext}$

Definition 1. The extension functor $\mathrm{Ext}_{\mathcal{A}}^{n}(-,B)$ is given by right derived functor of $\mathrm{Hom}_{\mathcal{A}}(-,B)$ , the controvariant functor. I.e. $\mathrm{Ext}_{\mathcal{A}}^{n}(-,B)=R^{n}\mathrm{Hom}_{\mathcal{A}}(-,B)$ .

Since $\mathrm{Hom}(-,B)$ is a left exact functor, $\mathrm{Ext}_{\mathcal{A}}^{0}(A,B)\cong \mathrm{Hom}(A,B)$ , by theorem in Derived Functors.

Proposition 1. If $P$ is projective, $I$ is injective, then $\mathrm{Ext}_{\mathcal{A}}^{n}(P,B)=\mathrm{Ext}_{\mathcal{A}}^{n}(A,I)=0$ .

Proof

Proof. For projective resolution $O\to P$ , we have

\mathrm{Ext}_{\mathcal{A}}^{n}(P,B)=H^{n}(\mathrm{Hom}(O,B))=0

For $\mathrm{Ext}_{\mathcal{A}}^{n}(A,I)$ , we check that $\mathrm{Hom}(-,I)$ is an exact functor. Only need to show for exact sequence $0\to A\to B\to C\to 0$ , $\mathrm{Hom}(B,I)\to \mathrm{Hom}(A,I)\to 0$ exact. This is directly from the injectivity. So $\mathrm{Hom}(-,A)$ is exact, and $R^{n}\mathrm{Hom}(-,I)=0$ for all $n\geq 1$ . ◻

Proposition 2. For any exact sequence $0\to B'\to B\to B''\to 0$ and object $A$ , we have the long exact sequence

\cdots\to\mathrm{Ext}_{\mathcal{A}}^{n}(A,B')\to \mathrm{Ext}_{\mathcal{A}}^{n}(A,B)\to \mathrm{Ext}_{\mathcal{A}}^{n}(A,B'')\to \mathrm{Ext}_{\mathcal{A}}^{n+1}(A,B')\to \cdots

Proof

Proof. Immediate corollary from Derived Functors ◻

Functor $\bar{\mathrm{Ext}}$

Definition 2. The extension functor $\bar{\mathrm{Ext}}_{\mathcal{A}}^{n}(A,-)$ is given by the right derived functor of $\mathrm{Hom}_{\mathcal{A}}(A,-)$ , the covariant functor, i.e. $\bar{\mathrm{Ext}}_{\mathcal{A}}^{n}(A,-)=R^{n}\mathrm{Hom}_{\mathcal{A}}(A,-)$ .

$\mathrm{Hom}(A,-)$ is a left exact functor so $\bar{\mathrm{Ext}}_{\mathcal{A}}^{0}(A,B)=\mathrm{Hom}(A,B)$ .

Theorem 1. The bifunctor $\mathrm{Ext}_{\mathcal{A}}^{n}(-,-)$ and $\bar{\mathrm{Ext}}_{\mathcal{A}}^{n}(-,-)$ are naturally equivalent.

Proof

Proof. We use induction to show $\mathrm{Ext}_{\mathcal{A}}^{n}(-,-)\cong \bar{\mathrm{Ext}}_{\mathcal{A}}^{n}(-,-)$ .

For $n=1$ , take an injective presentation $0\to B\to I\to S\to 0$ of $B$ and a projective resolution $P$ of $A$ . Since $P_{n}$ are all projective, we have

0\to \mathrm{Hom}(P,B)\to \mathrm{Hom}(P,I)\to\mathrm{Hom}(P,S)\to 0

exact. Applying the right derived functor, we get

\mathrm{Hom}(A,I)\to \mathrm{Hom}(A,S)\to\mathrm{Ext}_{\mathcal{A}}^{1}(A,B)\to 0=\mathrm{Ext}_{\mathcal{A}}^{1}(A,I)

exact. Derive the exact sequence $0\to B\to I\to S\to 0$ , we also have the exact sequence

\mathrm{Hom}(A,I)\to \mathrm{Hom}(A,S)\to\mathrm{Ext}_{\mathcal{A}}^{1}(A,B)\to 0=\bar{\mathrm{Ext}}_{\mathcal{A}}^{1}(A,I)

From the above two exact sequence, $\mathrm{Ext}_{\mathcal{A}}^{1}(A,B)\cong \bar{\mathrm{Ext}}_{\mathcal{A}}^{1}(A,B)$ .

For $n\geq 2$ , just replace these two exact sequence by

\bar{\mathrm{Ext}}_{\mathcal{A}}^{n-1}(A,I)\to \bar{\mathrm{Ext}}_{\mathcal{A}}^{n-1}(A,S)\to \bar{\mathrm{Ext}}_{\mathcal{A}^{n}}(A,B)\to \bar{\mathrm{Ext}}_{\mathcal{A}}^{n}(A,I)

and

\mathrm{Ext}_{\mathcal{A}}^{n-1}(A,I)\to \mathrm{Ext}_{\mathcal{A}}^{n-1}(A,S)\to \mathrm{Ext}_{\mathcal{A}}^{n}(A,B)\to \mathrm{Ext}_{\mathcal{A}}^{n}(A,I)

◻

For exact sequence $0\to R_{n-1}\to P_{n-1}\to \cdots\to P_{0}\to A\to 0$ , where $P_{n-1},\dots, P_{0}$ are all projective, then

\mathrm{Ext}_{\mathcal{A}}^{n}(A,B)=\mathrm{Coker}(\mathrm{Hom}(P_{n-1},B)\to \mathrm{Hom}(R_{n-1},B))

For exact sequence $0\to B\to I_{0}\to \cdots\to I_{n-1}\to S_{n-1}\to 0$ , where $I_{0},\dots, I_{n-1}$ are all injective, then

\mathrm{Ext}_{\mathcal{A}}^{n}(A,B)=\mathrm{Coker}(\mathrm{Hom}(A,I_{n-1})\to \mathrm{Hom}(A,S_{n-1}))

These are the corollary of theorem in Derived Functors

Functor $\mathrm{Tor}$

Definition 3. The torsion functor $\mathrm{Tor}_{n}^{\mathcal{A}}(A,-)$ is given by the left derived functor of the covariant functor $A\otimes_{\mathcal{A}}-$ , i.e. $\mathrm{Tor}_{n}^{\mathcal{A}}(A,-)=L_{n}(A\otimes_{\mathcal{A}}-)$ .

Since $A\otimes -$ is a right exact functor, we have $\mathrm{Tor}^{\mathcal{A}}_{0}(A,B)=A\otimes B$ .

Similarly, we can define $\bar{\mathrm{Tor}}^{\mathcal{A}}_{n}(-,B)=L_{n}(-\otimes B)$ , here $-\otimes B$ is a covariant functor.

Theorem 2. The bifunctor $\mathrm{Tor}^{\mathcal{A}}_{n}(-,-)$ and $\bar{\mathrm{Tor}}^{\mathcal{A}}_{n}(-,-)$ are naturally equivalent.

Proof

Proof. Similar to the proof of $\mathrm{Ext}$ and $\bar{\mathrm{Ext}}$ above. Note that every projective module is flat. ◻

Similary to functor $\mathrm{Ext}$ , we have following conclusions. For the exact sequence $0\to R_{n-1}\to P_{n-1}\to \cdots\to P_{0}\to A\to 0$ , where $P_{n-1},\dots, P_{0}$ are all projective, then

\mathrm{Tor}^{\mathcal{A}}_{n}(A,B)=\mathrm{Ker}(R_{n-1}\otimes B\to P_{n-1}\otimes B)

For the exact sequence $0\to R_{n-1}\to P_{n-1}\to \cdots\to P_{0}\to B\to 0$ , where $P_{n-1},\dots, P_{0}$ are all projective, then

\mathrm{Tor}^{\mathcal{A}}_{n}(A,B)=\mathrm{Ker}(A\otimes R_{n-1}\to A\otimes P_{n-1})

Proposition 3. If $A$ is flat, then for any object $P$ , $\mathrm{Tor}^{\mathcal{A}}_{n}(A,B)=0$ . Similar for flat $B$ .

Proof

Proof. For projective resolution $P\to B\to 0$ , $A\otimes P\to A\otimes B\to 0$ is also exact. Thus $\mathrm{Tor}^{\mathcal{A}}_{n}(A,B)=0$ . ◻

Theorem 3. If object $A$ has flat resolution $F\to A\to 0$ ,

$$F\quad \cdots\to F_{2}\to F_{1}\to F_{0}$$

then $\mathrm{Tor}^{\mathcal{A}}_{n}(A,B)=H_{n}(F\otimes B)$

Proof

Proof. We omit this proof and just use it. ◻

Computation fo $\mathrm{Ext}$ and $\mathrm{Tor}$

Theorem 4.

$\mathrm{Hom}(\oplus_{i} A_{i},\prod_{j}B_{j})=\prod_{i,j}\mathrm{Hom}(A_{i},B_{j})$ .
$\mathrm{Ext}_{\mathcal{A}}^{n}(\oplus_{i}A_{i},\prod_{j}B_{j})=\prod_{i,j}\mathrm{Ext}_{\mathcal{A}}^{n}(A_{i},B_{j})$ .
$(\oplus_{i}A_{i})\otimes (\oplus_{j}B_{j})=\oplus_{i,j}(A_{i}\otimes B_{j})$ .
$\mathrm{Tor}^{\mathcal{A}}_{n}(\oplus_{i}A_{i},\oplus_{j}B_{j})=\oplus_{i,j}\mathrm{Tor}^{\mathcal{A}}_{n}(A_{i},B_{j})$ .

Proof

Proof. Omitted. ◻

Now we focus on $\mathbb{Z}$ - $\mathrm{Mod}$ , $Z_{n}$ - $\mathrm{Mod}$ , $\mathbb{Q}$ - $\mathrm{Mod}$ and $\mathbb{Q /Z}$ - $\mathrm{Mod}$ .

For $\mathrm{Hom}$ , we have

$\mathrm{Hom}(\downarrow,\rightarrow)$	$Z_{m}$	$\mathbb{Z}$	$\mathbb{Q}$	$\mathbb{Q/Z}$
$Z_n$	$Z_{(m,n)}$	$0$	$0$	$Z_n$
$\mathbb{Z}$	$Z_m$	$\mathbb{Z}$	$\mathbb{Q}$	$\mathbb{Q/Z}$
$\mathbb{Q}$	$0$	$0$	$\mathbb{Q}$	?
$\mathbb{Q/Z}$	$0$	$0$	$0$	?

For $\mathrm{Ext}$ , we have

$\mathrm{Ext}(\downarrow,\rightarrow)$	$Z_{m}$	$\mathbb{Z}$	$\mathbb{Q}$	$\mathbb{Q/Z}$
$Z_n$	$Z_{(m,n)}$	$Z_n$	$0$	$0$
$\mathbb{Z}$	$0$	$0$	$0$	$0$
$\mathbb{Q}$	?	?	$0$	$0$
$\mathbb{Q/Z}$	?	?	$0$	$0$

For $\otimes$ , we have

$\downarrow\otimes_{\mathbb{Z}}\rightarrow$	$Z_{m}$	$\mathbb{Z}$	$\mathbb{Q}$	$\mathbb{Q/Z}$
$Z_n$	$Z_{(m,n)}$	$Z_n$	$0$	$0$
$\mathbb{Z}$	$Z_m$	$\mathbb{Z}$	$\mathbb{Q}$	$\mathbb{Q/Z}$
$\mathbb{Q}$	$0$	$\mathbb{Q}$	$\mathbb{Q}$	$0$
$\mathbb{Q/Z}$	$0$	$\mathbb{Q/Z}$	$0$	$0$

For $\mathrm{Tor}$ , we have

$\mathrm{Tor}(\downarrow,\rightarrow)$	$Z_{m}$	$\mathbb{Z}$	$\mathbb{Q}$	$\mathbb{Q/Z}$
$Z_n$	$Z_{(m,n)}$	$0$	$0$	$Z_n$
$\mathbb{Z}$	$0$	$0$	$0$	$0$
$\mathbb{Q}$	$0$	$0$	$0$	$0$
$\mathbb{Q/Z}$	$Z_m$	$0$	$0$	$\mathbb{Q/Z}$

And for those arbitrary abelian group, just apply the structure theorem of finite generated abelian group.

Ext functor and Tor functor

Functor Ext\mathrm{Ext}Ext

Functor Extˉ\bar{\mathrm{Ext}}Extˉ

Functor Tor\mathrm{Tor}Tor

Computation fo Ext\mathrm{Ext}Ext and Tor\mathrm{Tor}Tor

Functor $\mathrm{Ext}$

Functor $\bar{\mathrm{Ext}}$

Functor $\mathrm{Tor}$

Computation fo $\mathrm{Ext}$ and $\mathrm{Tor}$